Suppose That a Continuous Random Variable X Has the Density Function
Continuous Probability Distributions
(Continuous Random Variables)
Continuous random variables are used to model continuous phenomena or quantities, such as time, length, mass, ... that depend on chance.
We refer to continuous random variables with capital letters, typically \(X\), \(Y\), \(Z\), ... .
For instance the heights of people selected at ranom would correspond to possible values of the continuous random variable \(X\) defined as:
Probability Distributions
When working with continuous random variables, such as \(X\), we only calculate the probability that \(X\) lie within a certain interval; like \(P\begin{pmatrix}X \leq k\end{pmatrix}\) or \(P\begin{pmatrix}a\leq X \leq b \end{pmatrix}\).
We don't calculate the probability of \(X\) being equal to a specific value \(k\). In fact that following result will always be true: \[P\begin{pmatrix}X = k \end{pmatrix} = 0\] This can be explained by the fact that the total number of possible values of a continuous random variable \(X\) is infinite, so the likelihood of any one single outcome tends towards \(0\).
Calculating Probabilities
To calculate probabilities we'll need two functions:
- The probability density function (PDF)
- The cumulative density function (CDF) a.k.a the cumulative distribution function
Each of these is defined, further down, but the idea is to integrate the probability density function \(f(x)\) to define a new function \(F(x)\), known as the cumulative density function.
To calculate the probability that \(X\) be within a certain range, say \(a \leq X \leq b\), we calculate \(F(b) - F(a)\), using the cumulative density function.
Put "simply" we calculate probabilities as: \[P\begin{pmatrix}a\leq X \leq b \end{pmatrix} = \int_a^b f(x) dx\] where \(f(x)\) is the variable's probability density function.
Tutorial
In the following tutorial we learn about continuous random variables and how to calculate probabilities using probability density functions .
Exam Hint
We'll often be given a pdf with an unknown parameter that we'll need to find using the second property (see question 2.a below).
Properties of the PDF
Probability density functions are always greater than or equal to \(0\): \[f(x) \geq 0, \quad x \in \mathbb{R}\] The area enclosed by a probability density function and the horizontal axis equals to \(1\): \[\int_{-\infty}^{+\infty}f(x)dx = 1\] If the area isn't equal to \(1\) then \(X\) is not a continuous random variable.
Note: these properties are often used in exam questions.
Examples
Example 1
The piecewise function defined as: \[f(x) = \begin{cases} 3x^2,\quad 0\leq x \leq 1 \\ 0, \quad \text{elsewhere} \end{cases}\] could be the probability density function for some continuous random variable \(X\).
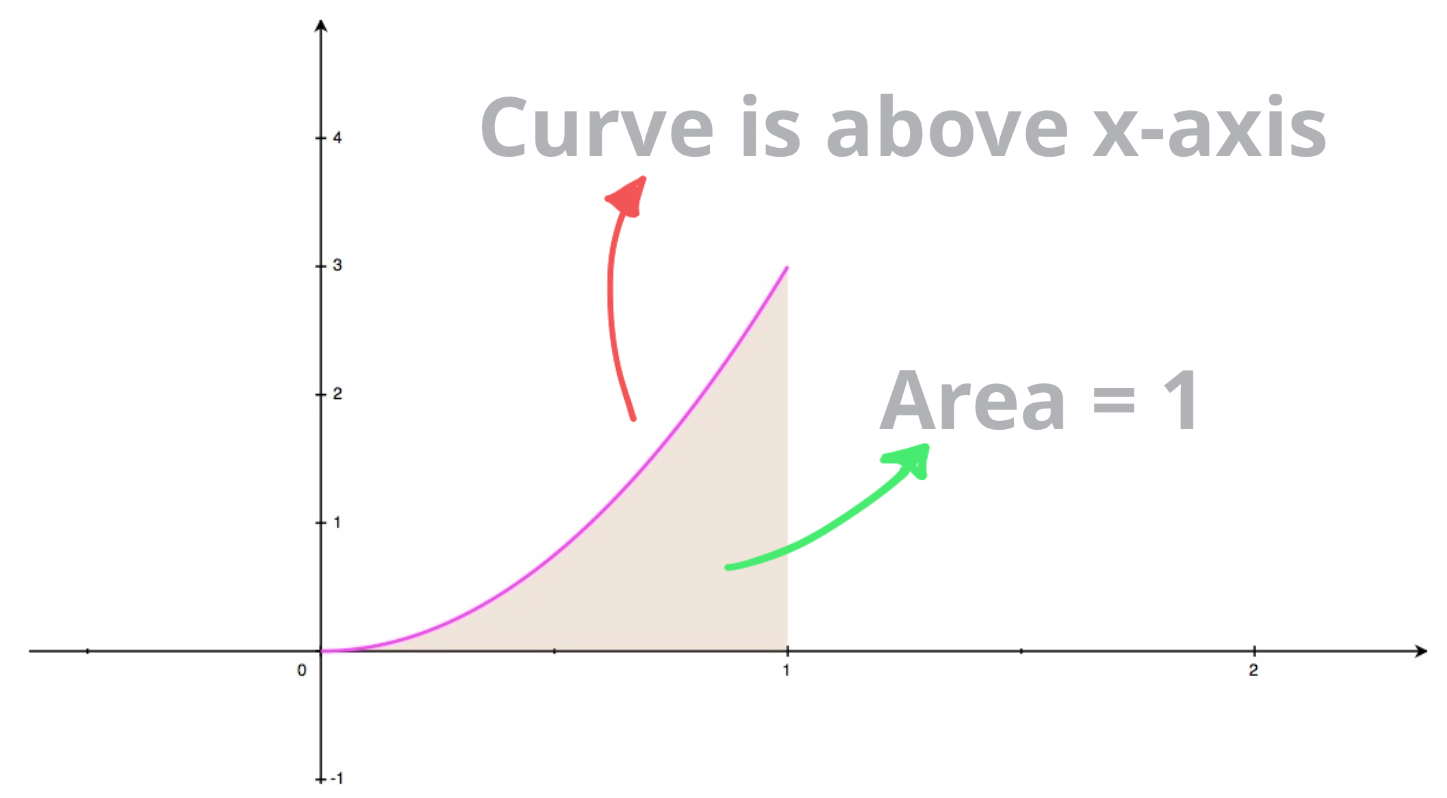 Indeed, we can see from its graph that \(f(x)\geq 0\). Furthermore we can check that the area enclosed by the curve and the \(x\)-axis equals to \(1\): \[\begin{aligned} \int_{-\infty}^{+\infty}f(x)dx & = \int_0^13x^2dx \\ & = \begin{bmatrix}x^3 \end{bmatrix}_0^1 \\ & = 1^3 - 0^3 \\ \int_{-\infty}^{+\infty}f(x)dx & = 1 \end{aligned}\]
Indeed, we can see from its graph that \(f(x)\geq 0\). Furthermore we can check that the area enclosed by the curve and the \(x\)-axis equals to \(1\): \[\begin{aligned} \int_{-\infty}^{+\infty}f(x)dx & = \int_0^13x^2dx \\ & = \begin{bmatrix}x^3 \end{bmatrix}_0^1 \\ & = 1^3 - 0^3 \\ \int_{-\infty}^{+\infty}f(x)dx & = 1 \end{aligned}\]
Example 2
Another example, that we'll learn about with normal distributions, could be the function defined as: \[f(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}, \quad x \in \mathbb{R}\]
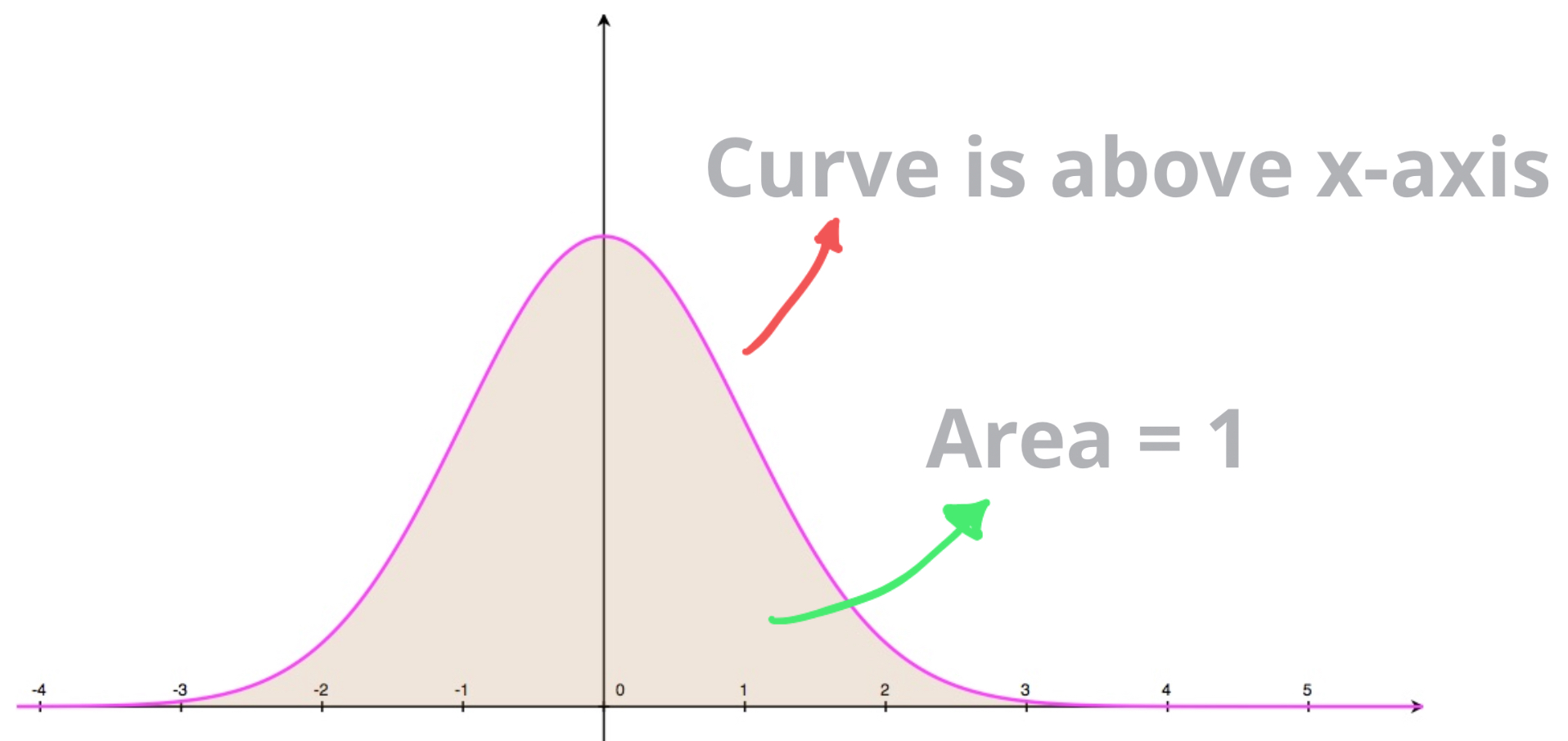 We can see from its graph that \(f(x)\geq 0\). And although we cannot integrate this by hand, use numerical methods and our calculator we find: \[\int_{-\infty}^{+\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx = 1\]
We can see from its graph that \(f(x)\geq 0\). And although we cannot integrate this by hand, use numerical methods and our calculator we find: \[\int_{-\infty}^{+\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx = 1\]
Terminology
Keep in mind that the Cumulative density function is frequently called the cumulative distribution function or simply the distribution function .
It's important to know that all \(3\) names refer to the same thing: the CDF.
Cumulative Density Function (CDF)
(Calculating Probabilities)
Given a continuous random variable \(X\) and its probability density function \(f(x)\), the cumulative density function , written \(F(x)\), allows us to calculate the probability that \(X\) be less than, or equal to, any value of \(x\), in other words: \(P\begin{pmatrix}X \leq x \end{pmatrix} = F(x)\).
Where: \[F(x) =\int_{-\infty}^x f(t)dt \] There are three "types" of probability calculations that we'll need to be comfortable with. Each is shown here:
Calculating \(P\begin{pmatrix}X \leq k \end{pmatrix}\)
Since \(F(x) = P\begin{pmatrix}X \leq x \end{pmatrix}\) we write: \[P\begin{pmatrix}X\leq k \end{pmatrix} = \int_{-\infty}^k f(x)dx\] This "tells us" that the probability that the continuous random variable \(X\) be less than or equal to some value \(k\) equals to the area enclosed by the probability density function and the horizontal axis, between \(-\infty \) and \(k\).
Calculating \(P\begin{pmatrix}a \leq X \leq b \end{pmatrix}\)
To calculate the probability that a continuous random variable \(X\), lie between two values say \(a\) and \(b\) we use the following result: \[P\begin{pmatrix}a \leq X \leq b \end{pmatrix} = \int_a^b f(x)dx\]
Calculating \(P\begin{pmatrix} X \geq k \end{pmatrix}\)
To calculate the probability that a continuous random variable \(X\) be greater than some value \(k\) we use the following result: \[P\begin{pmatrix} X \geq k \end{pmatrix} = \int_k^{+\infty} f(x)dx\]
Source: https://www.radfordmathematics.com/probabilities-and-statistics/continuous-probability-distributions/continuous-random-variables-probability-ditributions/probability-density-functions-continuous-random-variables.html
0 Response to "Suppose That a Continuous Random Variable X Has the Density Function"
Post a Comment